Research

I was first introduced to non-linear dynamics and biophysics as a sophomore undergraduate at IIT Bombay in a course taught by Amitabha Nandi and meandered around in the fields of biophysics and statistical physics before converging onto computational neuroscience and deep learning research with Ila Fiete. I have since moved on to pure deep learning research.

Building understanding in large-scale deep networks

I am also interested in understanding how large deep network models trained on extremely large amounts of data learn interesting representations, seeming capable of human-like behavior and what insights we can obtain by studying and reverse engineering them.

Previously, I was interested in neurodevelopment:

What is Computational NeuroDevelopment?

When an organism is born, its brain is already capable of complex computations despite not having any exposure to the real world. Biological brains can learn orders of magnitude faster and with much less experience than our best models. How does this happen? These are the questions that I like to think about.

I am interested in how biology builds powerful structured priors in neural circuits in the brain through the process of development and how we can best understand the mechanisms that underlie them. Often, developmental forces take the form of simple bottom-up processes & rules and ideas inspired from physics and biophysics come of use.

I am also interested in how similar structures can be incorporated into artificial neural networks. I believe this will speed up learning and improve generalization, bringing ANNs closer to human-like intelligence and will help clarify the relationship between the two.

This list is not updated, look at the google scholar or resume for a list of publications.

Publications

From smooth cortical gradients to discrete modules: spontaneous and topologically robust emergence of modularity in grid cells

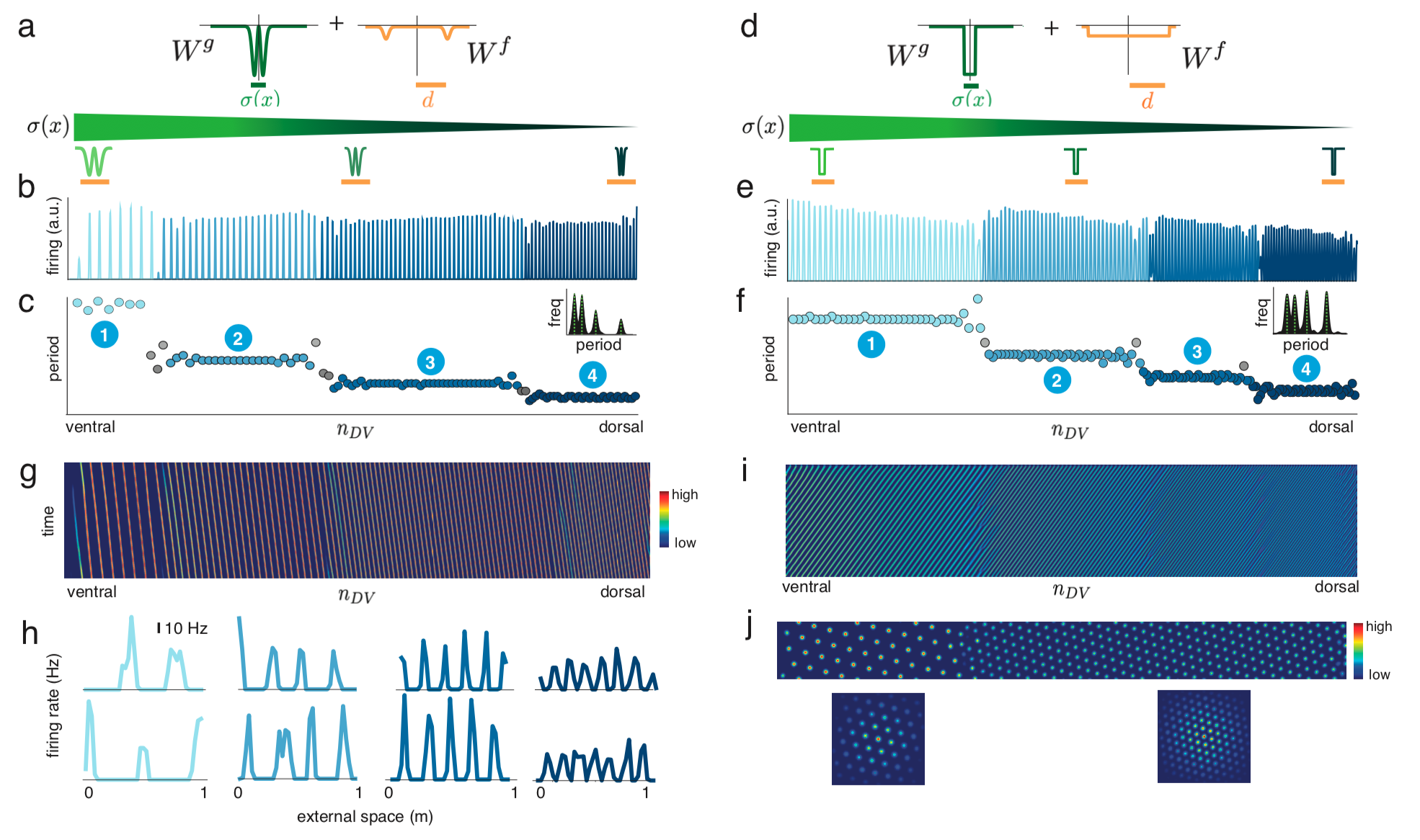Modular structures in the brain play a central role in compositionality and intelligence, however the general mechanisms driving module emergence have remained elusive. Studying entorhinal grid cells as paradigmatic examples of modular architecture and function, we demonstrate the spontaneous emergence of a small number of discrete spatial and functional modules from an interplay between continuously varying lateral interactions generated by smooth cortical gradients. We derive a comprehensive analytic theory of modularization, revealing that the process is highly generic with its robustness deriving from topological origins. The theory generates universal predictions for the sequence of grid period ratios, furnishing the most accurate explanation of grid cell data to date. Altogether, this work reveals novel principles by which simple bottom-up dynamical interactions lead to macroscopic modular organization.

Reverse-engineering recurrent neural network solutions to a hierarchical inference task for mice

Attractor and integrator networks in neuroscience